South Bay Simulations, Inc. |
|
|
SPLASH
|
South Bay Simulations, Inc. |
|
|
SPLASH
|
|
INTRODUCTION
South Bay Simulations conducted an in-house study to evaluate the applicability of the SPLASH free-surface panel code to catamaran hulls. The study was carried out after coming accros a draft of a paper entitled "Wave Resistance for High Speed Catamaran" by H.B. Moraes, J.M. Vasconcellos and R.G. Latorre, located at the web site: For routine free to sink and trim or nonlinear free-surface calculations, automated tools are required to iteratively update the panel model flotation and free-surface panel elevations. While such tools are available for SPLASH for a variety of monohulls (America's Cup or Volvo-60 yachts, IMS yachts, simple ships, etc.), automated tools have yet to be developed for SPLASH for multihull configurations. The SPLASH catamaran calculations reported here were limited to those which could be made utilizing existing capabilities, which for catamarans means using manually generated models, at fixed sink and trim, and with flat free-surface panels (thus resulting in a double-body-linearized type of free-surface boundary condition). Moraes, et. al., presented model-free results for monohulls at high speed and in deep and shallow water. Similar SPLASH calculations for monohulls were easily made using the already existing free to sink and trim and nonlinear free-surface automated tools for monohulls, thus providing additional relevant comparisons. CATAMARAN RESULTS Comparisons were made with the results presented by Moraes, et. al., for catamarans using Wigley parabolic hullforms. The SPLASH panel models were very simple, with even panel spacing throughout, and rectangular free-surface panel topologies extending 1/2 boat length in each direction from the hulls (upstream, downstream and to the sides). A total of 48 panels were located along the hull length. Being manualy generated and using flat free-surface panels, these panelizations were for models fixed in sink and trim, and the corresponding SPLASH calculations employed a double-body-linearized type of free-surface boundary condition. Four values of catamaran hull separation distances were modeled, corresponding to four values of S/L (the ratio of hull separation distance S to hull length L). The values of S/L considered were 0.2, 0.4, 1.0 and infinite (i.e., the monohull case). Also of note, the SPLASH catamaran models featured wakes shedding off the vertical stem at the stern of the Wigley hullforms, thus the reported SPLASH wave drags include vortex and wave drag due to the lift (side force) acting on each hull. The figure below shows the SPLASH-computed wave fields for the hull separation distances considered. The independence of each hull's wave field at S/L=1.0 is evident, as is the merging of the wave fields from the two hulls as separation distance decreases.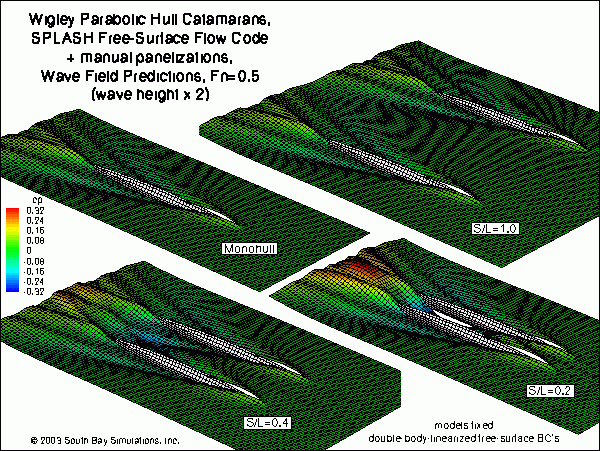 
click here for a high-quality pdf file format (1.53 MB)
The corresponding SPLASH wave drag predictions are given in the figure below, along with those presented by Moraes, et. al., which include three separate sets of results: the earlier slender body results of Millward, their own slender body results, and their results obtained using ShipFlow, a competitor potential flow free-surface panel code. Each of the prediction methods gives somewhat different results. The SPLASH results appear to be quite well behaved, without any extreme trending or oscillation (except the usual low-speed humps), and seem to correlate reasonably well with both sets of slender body results. In comparison, the ShipFlow results appear less consistent and more extreme in value, particularly with regard to the detailed effects of separation distance S/L. It is not yet known if the ShipFlow results obtained by Moraes, et. al., included a nonlinear free-surface boundary condition, which might account for the large discrepancies between the ShipFlow results versus the SPLASH and slender body results. However, consideration of all the comparisons presented herein (particularly the wetted area results for the Wigley monohull when free to sink and trim) indicate that the ShipFlow results were probably obtained using some type of linear free-surface boundary condition. The less consistent and more extreme quality of the ShipFlow predictions are therefore likely not due to any nonlinear free-surface effects.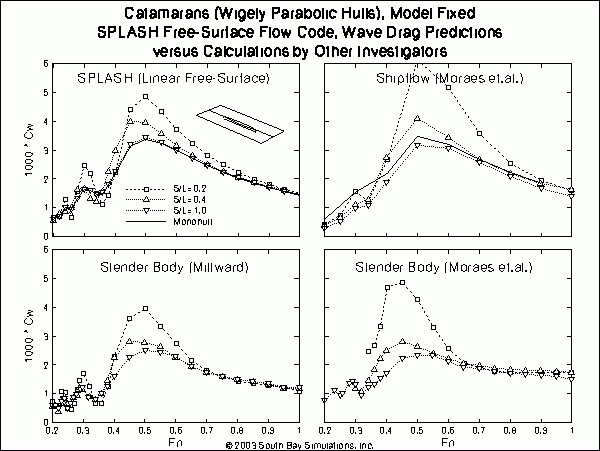 
click here for a high-quality pdf file format (37.5 KB)
The only other Wigley model-fixed results presented by Moraes, et. al., are ShipFlow results for the effect of shallow water on monohull wave drag. Corresponding SPLASH predictions are compared to the ShipFlow results in the figure below. While there is reasonable agreement beteeen SPLASH and ShipFlow in the overall trend between deep water and shallow water, one noticeable difference is the ShipFlow prediction of a distinct dip in wave drag at a Froude number of 0.6 due to the shallow water effect which does not appear in the SPLASH results. Perhaps there are other results available, experimental or analytical, to shed light on which is the more correct shallow water effect?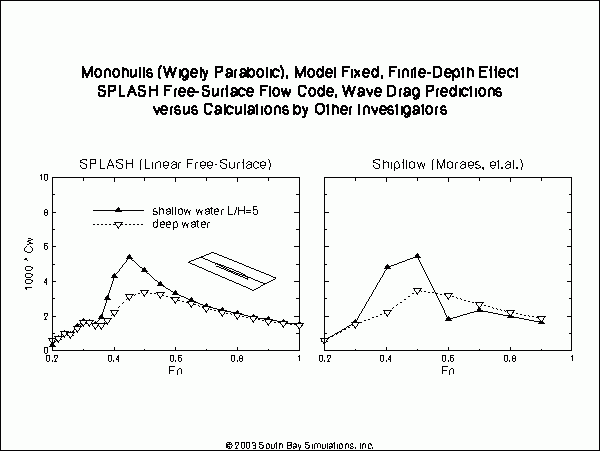 
click here for a high-quality pdf file format (14.3 KB)
RELATED MONOHULL RESULTS Related comparisons were made with the model-fixed and model-free results presented by Moraes, et. al., for monohulls using Wigley parabolic hullform in deep and shallow water. For these cases, SPLASH was run using the automated tools specific to monohulls, thus results were readily obtained for both model-fixed and model-free to sink and trim, and for both linear and nonlinear type of free-surface boundary condition. The SPLASH panel models were again very simple, at least compared to the automated models typically generated for fully appended yachts at heel and yaw. In contrast to the rectangular free-surface panelizations used to generate the SPLASH results in the preceeding section, the automated tools for monohulls use a pebble-in-pond panelization of the free-surface. Free-surface panel topologies extended 3/4 boat length in each direction from the hull (upstream, downstream and to the sides). A total of 55 panels were located along the hull length. The figure below shows the SPLASH-computed nonlinear wave fields for the monohull, free to sink and trim, and in deep water and in shallow water. A visual inspection suggests that the shallow water effect is to intensify the bow wave and midbody trough, and to decrease the magnitude of the stern wave. As implemented in the automated tools, the pebble-in-pond free-surface panelization does not provide high resolution except local to the hull. This produces a rapid decay of waves moving away from the vessel, and so the approach is not well suited to capturing the trailing Kelvin wave field. Nevertheless, in the immediate vicinity of the hull, the deep-water wave field appears to be the same as that shown in the preceeding section and generated using a rectangular free-surface topology.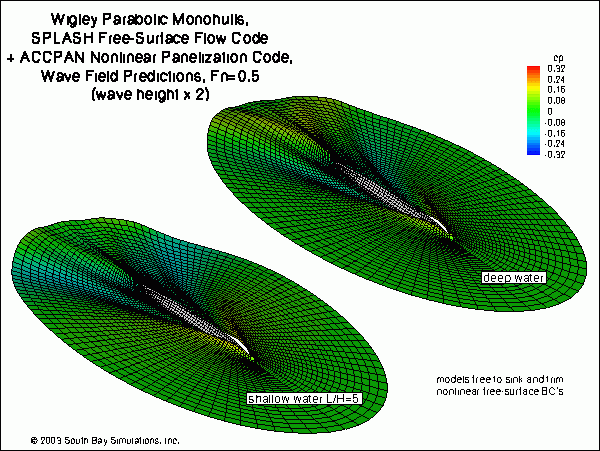 
click here for a high-quality pdf file format (0.50 MB)
Associated SPLASH predictions were obtained using both linear and nonlinear free-surface boundary conditions, and compared to those of Moraes, et. al., using ShipFlow. Wave drag predictions for the model-fixed are given in the figure below. The SPLASH linear free-surface predictions show excellent, although not exact, agreement with the corresponding results from the preceeding section and generated using a rectangular free-surface topology. The SPLASH nonlinear free-surface predictions are qualitatively very similar to the linear ones. The overall magnitude of the nonlinear results appear slightly smaller at lower Froude numbers and slightly larger at higher Foude numbers. The ShipFlow results are the same as those discussed in the previous section, and so the previous comments regarding SPLASH versus Shipflow apply here as well.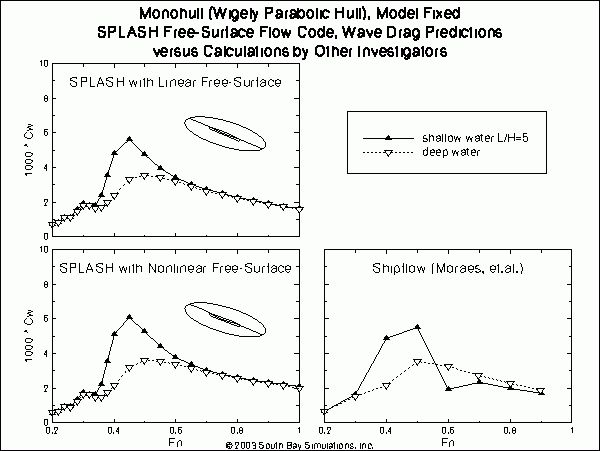 
click here for a high-quality pdf file format (19.6 KB)
Wave drag predictions for the model-free to sink and trim are given in the figure below. The results are not too dissimilar from the model-fixed results, although maximum wave drag levels (between Froude numbers of 0.4 to 0.5) increase, and the shallow water effect here produces a small but distinct reduction in drag at Froude numbers above 0.6. This shallow water effect is more pronounced in the nonlinear (versus linear) free-surface results. The ShipFlow results for the model-free condition are more extreme in magnitude than the SPLASH results, with the ShipFlow results again showing a distinct dip in wave drag at a Froude number of 0.6 due to the shallow water effect which does not appear in the SPLASH results.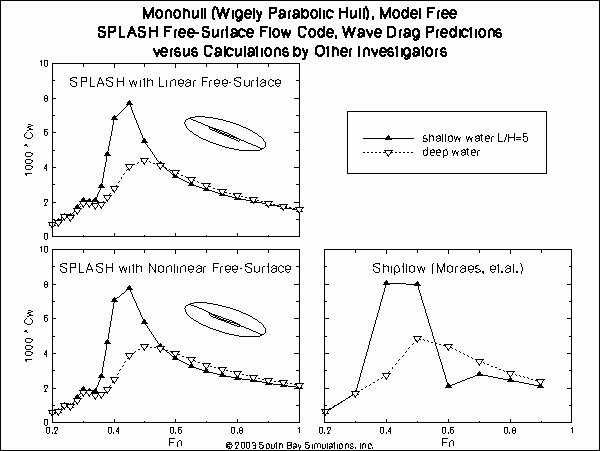 
click here for a high-quality pdf file format (19.7 KB)
ShipFlow results were also presented by Moraes, et. al., showing the percent change in hull wetted area. SPLASH wetted area results are compared to those using ShipFlow in the figure below. The SPLASH results show a very strong effect due to the nonlinear free-surface boundary conditions. The ShipFlow predictions are more similar to the SPLASH linear free-surface results, with some slightly different trending at higher speeds, as well as a dip at a Froude number of 0.6 in the ShipFlow results much the same as was observed in the ShipFlow wave drag predictions. All the SPLASH results presented here include waterline integral contributions to the forces and moments (these contributions should be very small for the SPLASH nonlinear solutions which, due to some smoothing of free-surface wave heights prior to free-surface repanelization, are not exactly nonlinear, just approximately so). Unfortunately, although the required elements are already available, no provision was implemented in SPLASH to account for the waterline integral contribution to the output wetted surface area. It is posssible that such a contribution to the linear results might reduce the discrepancy versus the nonlinear results. Perhaps there is available experimental data showing the wetted area variation for a Wigley parabolic monohull under free to sink and trim conditions? If so, comparison of these results with experimental data would be of great interest.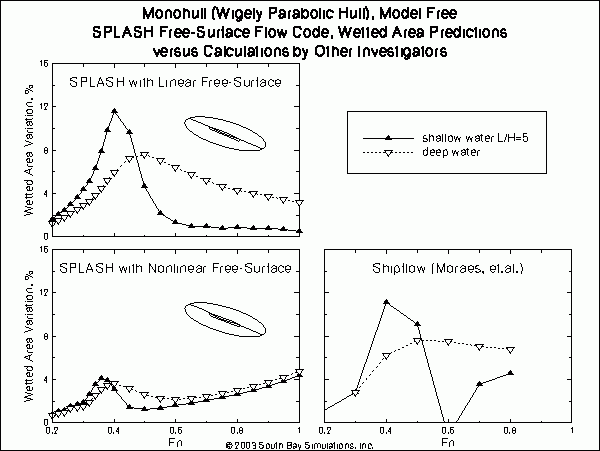 
click here for a high-quality pdf file format (19.5 KB)
Further ShipFlow results were presented by Moraes, et. al., showing the percent change in submerged volume. SPLASH submerged volume results are compared to those using ShipFlow in the figure below. To be more specific, it was not clear from Moraes, et. al., as to the meaning of submerged volume, especially in the case of nonlinear free-surface calculations. It was decided to compare the hydrodynamic vertical force (i.e., the suckdown force) as a percent of hull weight, as this is equivalent to the percent submerged volume, at least certainly in the case of linear free-surface calculations. There are some small but distinct differences between the linear and nonlinear SPLASH results. The ShipFlow results again show fair agreement with the SPLASH results, except again there is a distinct dip in the ShipFlow results at a Froude number of 0.6, and somewhat different final trending at the higher Froude numbers.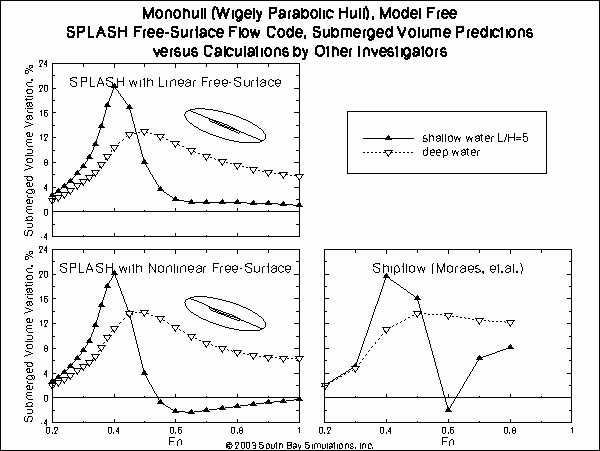 
click here for a high-quality pdf file format (20.3 KB)
CONCLUSIONS - AREAS REQUIRING FURTHER DEVELOPMENT For catamarans, major changes to the SPLASH free-surface panel code, i.e., to the flow solver, are not needed. What is required is developement of automated tools for iterative updating of: hull waterline and flotation; free-surface panel elevations; and the corresponding hull and free-surface panelizations. Only with such tools will it be possible to routinely obtain SPLASH results for catamaran hulls that are free to sink and trim, and including nonlinear free-surface effects. Developing automated tools for a simple hullform such as the Wigley parabolic would appear to be fairly straightforward. However certain aspects of bow and stern geometries will likely introduce greater levels of complexity. Consider the case where a bow stem is partially submerged at rest, but might rise nearly or completely above the water surface whilst underway (for example, due to dynamic sink and trim). Just this relatively simple additional consideration can introduce a great deal of complexity into the development of the required automated tools. There are similar considerations at the stern. Not to mention the possibility of a transom stern, which likewise may or may not be immersed whilst underway. Regarding transom sterns, SPLASH has the capabilities to approximate wet or dry transom flows. Over the years these have been implemented for a variety of applications ranging from Volvo-60 grand prix racing yachts, to tankers and cargo ships, to planing flat plates and skis. SPLASH also has a capability to approximate a hull with a wet chine, which was used to model the side edges of the planing flat plates and skis. Implicit in this dicussion is the assumption that, for a wide range of catamaran applications, heel angle is not an important consideration. So, at least to start, automated tools for catamarans in SPLASH could be developed more easily by considering upright, zero-heel cases only. Another area for potential development would be to incorporate appendages (foils, keels, daggerboards, rudders, hydrofoils, etc.) into the catamaran panel models, and into any automated tools that might be developed to facilitate and enhance their use in SPLASH. |
© 2009 South Bay Simulations, Inc.
